1.哈夫曼树介绍
在计算机数据处理中,霍夫曼编码使用变长编码表对源符号(如文件中的一个字母)进行编码,其中变长编码表是通过一种评估来源符号出现机率的方法得到的,出现机率高的字母使用较短的编码,反之出现机率低的则使用较长的编码,这便使编码之后的字符串的平均长度、期望值降低,从而达到无损压缩数据的目的。
例如,在英文中,e的出现机率最高,而z的出现概率则最低。当利用霍夫曼编码对一篇英文进行压缩时,e极有可能用一个比特来表示,而z则可能花去25个比特(不是26)。用普通的表示方法时,每个英文字母均占用一个字节(byte),即8个比特。二者相比,e使用了一般编码的1/8的长度,z则使用了3倍多。倘若我们能实现对于英文中各个字母出现概率的较准确的估算,就可以大幅度提高无损压缩的比例。
霍夫曼树又称最优二叉树,是一种带权路径长度最短的二叉树。所谓树的带权路径长度,就是树中所有的叶结点的权值乘上其到根结点的路径长度(若根结点为0层,叶结点到根结点的路径长度为叶结点的层数)。树的路径长度是从树根到每一结点的路径长度之和,记为WPL=(W1L1+W2L2+W3L3+...+WnLn),N个权值Wi(i=1,2,...n)构成一棵有N个叶结点的二叉树,相应的叶结点的路径长度为Li(i=1,2,...n)。可以证明霍夫曼树的WPL是最小的。
演算过程
进行霍夫曼编码前,我们先创建一个霍夫曼树。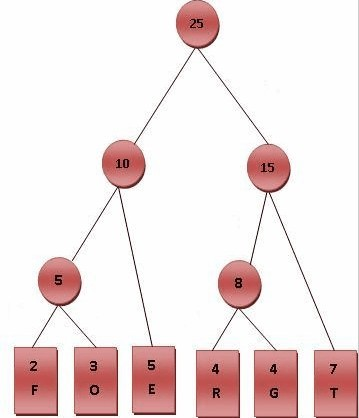
⒉每个字母都代表一个终端节点(叶节点),比较F.O.R.G.E.T五个字母中每个字母的出现频率,将最小的两个字母频率相加合成一个新的节点。如Fig.2所示,发现F与O的频率最小,故相加2+3=5。
⒊比较5.R.G.E.T,发现R与G的频率最小,故相加4+4=8。
⒋比较5.8.E.T,发现5与E的频率最小,故相加5+5=10。
⒌比较8.10.T,发现8与T的频率最小,故相加8+7=15。
⒍最后剩10.15,没有可以比较的对象,相加10+15=25。
进行编码
1.给霍夫曼树的所有左链结'0'与
霍夫曼树 霍夫曼树 右链结'1'。2.从树根至树叶依序记录所有字母的编码
2.实验内容
设有字符集:S={a,b,c,d,e,f,g,h,i,j,k,l,m,n.o.p.q,r,s,t,u,v,w,x,y,z}。
给定一个包含26个英文字母的文件,统计每个字符出现的概率,根据计算的概率构造一颗哈夫曼树。 并完成对英文文件的编码和解码。 要求: (1)准备一个包含26个英文字母的英文文件(可以不包含标点符号等),统计各个字符的概率 (2)构造哈夫曼树 (3)对英文文件进行编码,输出一个编码后的文件 (4)对编码文件进行解码,输出一个解码后的文件 (5)撰写博客记录实验的设计和实现过程,并将源代码传到码云 (6)把实验结果截图上传到云班课 满分:6分。 酌情打分。3. 实验过程及结果
HuffmanNode类 实现哈夫曼树的结点
public class HuffmanNode { private int weight;//权值 private int parent; private int leftChild; private int rightChild; public HuffmanNode(int weight,int parent,int leftChild,int rightChild){ this.weight=weight; this.parent=parent; this.leftChild=leftChild; this.rightChild=rightChild; } void setWeight(int weight){ this.weight=weight; } void setParent(int parent){ this.parent=parent; } void setLeftChild(int leftChild){ this.leftChild=leftChild; } void setRightChild(int rightChild){ this.rightChild=rightChild; } int getWeight(){ return weight; } int getParent(){ return parent; } int getLeftChild(){ return leftChild; } int getRightChild(){ return rightChild; }} HuffmanCode 类 记录所用的字符及对应的编码
public class HuffmanCode { private String character; private String code; HuffmanCode(String character,String code){ this.character=character; this.code=code; } HuffmanCode(String code){ this.code= code; } void setCharacter(String character){ this.character=character; } void setCode(String code){ this.code=code; } String getCharacter(){ return character; } String getCode(){ return code; }} HuffmanTree类,实现哈夫曼树以及每个符号获得对应的前缀码
public class HuffmanTree { //初始化一个huffuman树 public static void initHuffmanTree(HuffmanNode[] huffmanTree,int m){ for(int i=0;i =0 ) { start--; code[start]=((huffmanTree[parent].getLeftChild()==c)?'0':'1'); c=parent; } for(;start HuffmanTest类 读取相应的文件并做出加密解密操作
import java.io.*;import static week15.HuffmanTree.*;public class HuffmanTest { private char[] chars = new char[]{'a','b','c','d','e','f','g','h','i','j','k','l','m','n','o','p','q','r','s' ,'t','u','v','w','x','y','z'}; private int[] number = new int[]{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0}; public String txtString(File file){ StringBuilder result = new StringBuilder(); try{ BufferedReader br = new BufferedReader(new FileReader(file));//构造一个BufferedReader类来读取文件 String s = null; while((s = br.readLine())!=null){//使用readLine方法,一次读一行 result.append(System.lineSeparator()+s); num(s); } br.close(); }catch(Exception e){ e.printStackTrace(); } return result.toString(); } public void num(String string){ for(int i = 0;i<26;i++){ int temp = 0; for(int j = 0;j 3. 实验过程中遇到的问题和解决过程
问题1: 只输出了两个数的编码
只输出了两个数的编码
问题1解决方案:
 改正之后就没问题了
改正之后就没问题了